Voici les réponses aux différentes questions
Réponses
Réponse 1
La première réponse est très détaillée. Les autre réponses seront plus succinctes.
1 Les adresses
Pour effectuer un calcul, l’automate doit disposer de trois informations :
- l’instruction (l’opération)
- l’opérande 1
- l’opérande 2
Plus que ça, il doit en disposer en même temps. Mais elles sont stockées en RAM, et ne peuvent être lues que l’une après l’autre. Il faudra donc prévoir un moyen de stockage de ces trois informations à l’intérieur du processeur pour pouvoir effectuer le calcul.
Vu l’organisation de la mémoire, il semble logique de lire ces trois informations de la façon la plus simple possible, c’est à dire :
- tout d’abord l’instruction,
- puis l’opérande 1,
- puis l’opérande 2,
ce qui correspond à un parcours linéaire de la mémoire.
De plus, le stockage du résultat s’effectue dans la RAM à l’adresse suivant celle de l’opérande 2. On peut donc doter l’automate d’un compteur qu’on appellera compteur d’adresse ou PC (Program Counter), qui donnera l’adresse de la RAM à laquelle on est en train d’accéder (que ce soit en lecture ou en écriture). Ce compteur sera incrémenté à chaque coup d’horloge, et pilotera directement le bus d’adresse de la RAM.
2 Les données
Vu ce qui vient d’être dit, l’automate a un fonctionnement linéaire - l’ordre des actions effectuées est toujours le même :
- chercher une instruction
- chercher le premier opérande
- chercher la deuxième opérande
- stocker le résultat du calcul
On peut donc le concevoir comme un automate à quatre états, dont le fonctionnement est circulaire : état 1 → état 2 → état 3 → état 4 → état 1 → état 2 → …
État 1:
- le compteur est en train de présenter à la RAM une adresse correspondant à une instruction.
Le processeur récupère sur le bus Q[7:0] la contenu de la RAM à cette adresse, c’est à dire l’instruction à effectuer. - il faut stocker cette instruction pour plus tard (quand on effectuera l’opération demandée).
On ajoute donc à l’automate un registre sur 8 bits disposant d’un enable (8 bascules DFFE en parallèle).
L’entrée de ce registre est reliée au bus Q[7:0] (sortie de la RAM)
Le signal d’enable de ce registre est mis à l’état haut seulement pendant l’état 1 –> stockage de l’instruction dans le registre
État 2:
- le compteur est en train de présenter à la RAM une adresse correspondant aux premier opérande.
le processeur récupère sur le bus Q[7:0] la contenu de la RAM à cette adresse, c’est à dire l’opérande 1… - il faut stocker cet opérande, donc re-belotte, on ajoute un registre 8 bits avec enable, relié à la sortie de la RAM (Q[7:0]).
l’enable est mis à l’état haut seulement pendant l’état 2.
État 3:
- le compteur est en train de présenter à la RAM une adresse correspondant aux deuxième opérande.
le processeur récupère sur le bus Q[7:0] la contenu de la RAM à cette adresse, c’est à dire l’opérande 2… - comme d’habitude on stocke cet opérande dans un registre 8 bits, dont l’enable est piloté à l’état haut seulement pendant ce cycle-ci.
Remarque : on peut se dire que ce n’est pas la peine de stocker cet opérande, car on dispose dès à présent de toutes les données pour effectuer le calcul : l’instruction dans un registre, l’opérande dans un autre registre, et le deuxième opérande sur le bus Q[7:0]. Mais il faudrait alors stocker le résultat dans un registre 8 bits, car on ne fait son stockage en RAM qu’au prochain cycle…Alors qu’ici, le calcul et le stockage seront faits en bloc au prochain cycle (donc pas besoin de stocker le résultat dans un registre). Au total, dans les deux approches, le nombre de registres est le même, et ce ne sont que des considérations de chemin critique qui permettront de déterminer la meilleure des deux méthodes…
État 4:
- le compteur est en train de présenter à la RAM une adresse correspondant au résultat à stocker.
- l’automate dispose dans ses trois registres de toutes les données pour effectuer le calcul. Il suffit d’ajouter une fonction combinatoire pure, pour produire le résultat.
La sortie de cette fonction combinatoire sera reliée au bus d’entrée de la RAM.
L’équation de cette fonction sera du genre : RES[7:0] = (si INSTRUCTION="00000100" : OP_1[7:0] + OP_2[7:0], sinon OP_1[7:0] - OP_2[7:0])
Une telle fonction combinatoire a été réalisée au TP numéro 2…(ALU) - Parallèlement, l’automate doit piloter le signal WRITE de la RAM à l’état haut, pour dire à la RAM de stocker à l’adresse courante la sortie de la fonction de calcul.
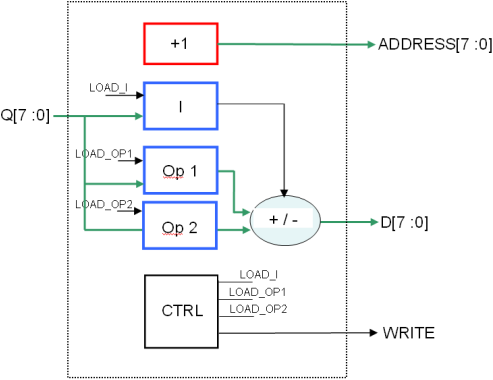
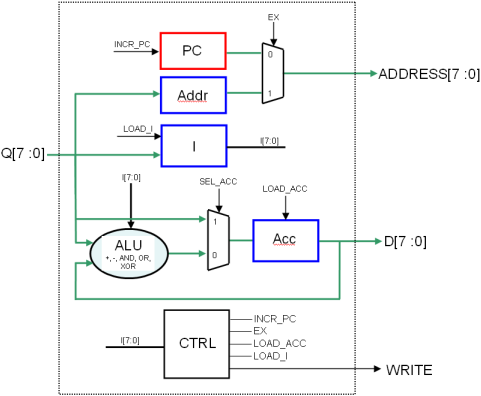
On obtient donc l’architecture suivante pour notre processeur :
- En rouge : le compteur d’adresse courante
- En bleu : les trois registres 8 bits, les signaux load sont les enable
- En noir rond : la fonction combinatoire de calcul proprement dite (ALU)
- En noir carré : la machine à état qui séquence tout ça…
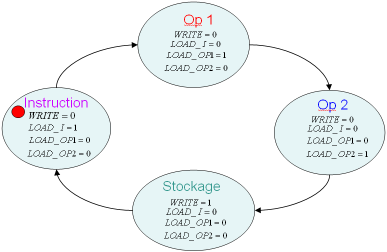
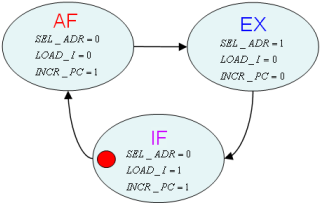
L'automate (CTRL) est présenté en figure 1.4 et son graphe d’états en figure 1.5.
L'automate a quatre états, parcourus de façon linéaire, sans condition sur les transitions.
Il dispose de 4 sorties, chacune d’entre elles à l’état haut dans un seul état de l'automate. Un codage "one-hot", consistant à matérialiser chaque état par un registre est donc très approprié.
L’implémentation en registre a déjà été vue (registres les uns à la suite des autres), et ne sera pas détaillée ici. Les sorties des registres donnent directement les sorties de l'automate…
Réponse 2
Plusieurs possibilités, leur nombre est limité seulement par votre imagination. Voici quelques exemples :
- Garder le résultat de chaque opération en mémoire, et définir une nouvelle addition qui opère sur un opérande en RAM et celle qu’on a gardé.
L’inconvénient est qu’on rajoute une instruction pour chaque type d’opération, que cette nouvelle opération, ne nécessitant qu’un seul opérande en RAM pourra être effectuée en 3 cycles au lieu de 4, et que ça risque de compliquer la machine à état si on veut l’optimiser (certaines opération en 3 cycles, d’autres en 4)… - Définir des opérations de manipulation de la RAM, et grâce à elles recopier le résultat en RAM à l’endroit d’une des deux opérandes de la prochaine instruction. C’est bien compliqué…
- Définir une nouvelle addition qui opère sur un opérande à l’endroit habituel en RAM, et sur un autre opérande situé à l’adresse (instruction - 1)…
- Utiliser la première solution, mais pour simplifier les choses (et par cohérence) supprimer les opérations sur deux opérandes en RAM. Toutes les opérations (à deux opérandes) se feront entre un opérande en RAM, et un gardé dans un registre interne au processeur. Et pour rendre cela possible, on définit deux nouvelles instructions : chargement de ce registre à partir d’une donnée en RAM, et stockage du contenu de ce registre en RAM. C’est l’objet de la suite !
Réponses 3 et 4
Chaque opération ne nécessite plus qu’un seul opérande :
- pour le load, c’est normal !
- pour le store, aucun opérande. Par contre, en RAM, à la suite de l’instruction store, il doit y avoir un emplacement libre pour stocker le contenu de l’accumulateur
- pour les opération à deux opérandes, l’un est en RAM, l’autre est interne à l’automate (c’est l’accumulateur)
Le contenu de la RAM se présentera donc maintenant ainsi :
| adresse | type du mot stocké | exemple | effet |
| 0 | instruction | load | |
| 1 | donnée | 3 | l’accumulateur contient maintenant 3 |
| 2 | instruction | + | |
| 3 | donnée | 4 | l’accumulateur contient maintenant 7 |
| 4 | instruction | - | |
| 5 | donnée | 1 | l’accumulateur contient maintenant 6 |
| 6 | instruction | store | |
| 7 | donnée | X | après l’exécution du programme cet emplacement en RAM contiendra “6” |
On remarque donc qu’une adresse sur deux contient une instruction, une sur deux contient une donnée (soit opérande, soit stockage du contenu de l’accumulateur)…
1 Les adresses
Comme précédemment, les adresses de la RAM sont parcourues de façon linéaire. On garde donc le compteur d’adresse incrémenté à chaque cycle d’horloge.
2 Les données
Pour effectuer les calculs, le processeur n’a plus besoin de connaître que deux informations : l’instruction et l’opérande. On garde donc le registre d’instruction (8 bits) qui stocke l’instruction à effectuer pendant qu’on va chercher l’opérande en RAM.
Par contre, auparavant on parcourait 4 emplacements en RAM pour chaque instructions, d’où une machine à états à 4 cycles. Maintenant on ne parcourt plus que 2 emplacements en RAM, donc une machine à état à 2 cycles devrait convenir…
A chaque instruction, le processeur effectuera ceci :
Pour une opération "normale" :
- aller chercher l’instruction en RAM, la stocker dans le registre d’instruction
- aller lire l’opérande en RAM, effectuer le calcul et stocker le résultat dans l’accumulateur (opération)
Pour un "load" :
- aller chercher l’instruction en RAM, la stocker dans le registre d’instruction
- aller lire l’opérande en RAM, et le stocker dans l’accumulateur (opération)
Pour un "store" :
- aller chercher l’instruction en RAM, la stocker dans le registre d’instruction
- écrire le contenu de l’accumulateur en RAM à l’adresse courante
Chaque instruction est donc traitée de façon très similaire :
- un cycle de récupération de l’instruction (dans lequel l’enable du registre d’instruction est mis à l’état haut).
- un cycle de traitement de l’instruction
3 L’accumulateur
Lors du second cycle, l’accumulateur peut subir trois traitements différents :
- pour une opération (+, −, AND, XOR, OR), l’accumulateur se voit modifié et chargé avec le résultat de l’opération
- pour un load, l’accumulateur est modifié aussi, et chargé avec la donnée sortant de la RAM
- pour un store par contre, l’accumulateur n’est pas modifié…
En entrée de l’accumulateur on mettra donc un multiplexeur qui présentera soit le résultat de l’opération en cours (si on exécute une opération standard), soit le contenu de la RAM (si on exécute un load). De plus, dans ces deux cas, le signal enable de l’accumulateur sera mis à l’état haut (pour autoriser sa modification) dans l’état 2 (quand on accède à la partie donnée de la RAM) Dans le cas d’un store, on laisse l’enable de l’accumulateur à l’état bas pour ne pas le modifier.
En d’autre termes, le signal de validation du chargement de l’accumulateur a pour équation en pseudo-langage :
LOAD_ACC = (Instruction <> STORE) ET (Etat = état 2)
Le pilotage du multiplexeur en entrée de l’accumulateur aura pour équation quelque chose du genre :
si (Instruction == LOAD) alors Q[7:0],
si (Instruction == opération) alors ALU(ACC, Q[7:0]),
si (Instruction == STORE) alors peu importe…)
Ce qui se simplifie en :
si (Instruction == LOAD) alors Q[7:0],
sinon ALU(ACC, Q[7:0]))
La sortie de l’accumulateur est branchée simultanément
- sur le bus d’entrée de la RAM (pour le cas d'une instruction "store")
- sur l’ALU (qui implémente, selon l’instruction à effectuer, l’addition, la soustraction, le XOR, etc…)
Enfin la génération du signal d’écriture en RAM est simple : il est mis à l’état haut quand l’instruction est un STORE, et qu’on est dans l’état 2. Le contenu de l’accumulateur est présenté sur l’entrée de la RAM (cf. ci dessus), l’adresse courante est sur le bus d’adresse de la RAM, la RAM est donc mise à jour avec la bonne valeur…
4 Bilan
Nous disposons donc les éléments suivants :
- compteur d’adresse (PC)
- registre d’instruction
- accumulateur avec multiplexeur en entrée
- un automate générant les signaux LOAD_I, LOAD_ACC, WRITE et le contrôle du multiplexeur
Remarque : Les signaux générés par l'automate ne dépendent pas seulement de l’état courant de l'automate, mais aussi de la nature de l’instruction à exécuter. On nomme ce genre d'automate "machine de Mealy")
L’architecture globale est celle représentée sur la figure 1.6, et son graphe d’états en figure 1.7
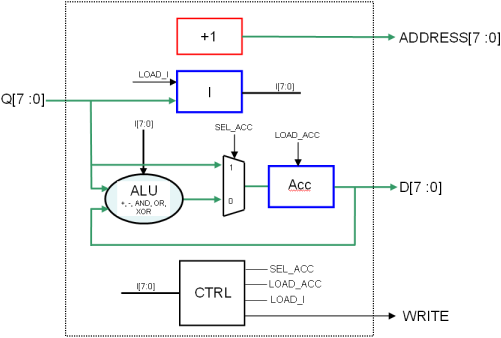
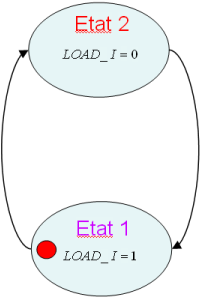
avec :
LOAD_ACC = (I[7:0] <> STORE) ET (Etat = état 2)
WRITE = (I[7:0] == STORE) ET (Etat = état 2)
5 Performances
Pour une opération :
- version 1 : 4 cycles
- version 2 : 6 cycles (2 + 2 + 2)
Pour deux opérations chaînées :
- version 1: 8 cycles (4 + 4. Enfin, plus exactement, on ne savait pas faire…)
- version 2: 8 cycles (2 + 2 + 2 + 2)
Pour trois opérations chaînées :
- version 1 : 12 cycles (4 + 4 + 4. Même remarque)
- version 2 : 10 cycles
Bref, pour n opérations :
- version 1: 4n cycles
- version 2 : 2n+4 cycles si peut les enchaîner, 3n sinon.
On a donc tout intérêt à enchaîner les calculs. Ce qui est très souvent le cas en pratique…
Réponse 5
L’automate doit maintenant pour chaque instruction
- aller chercher l’instruction (la stocker dans le registre d’instruction)
- aller chercher l’adresse de l’opérande (le stocker, dans un registre dit "d’adresse")
- aller chercher l’opérande proprement dit, en lisant la RAM à l’adresse stockée au cycle précédent.
On a donc une machine qui possède un état de plus (celui où on va lire en RAM l’opérande proprement dit).
1 Les adresses
Maintenant, on n’accède plus à la RAM de façon linéaire. Dans l’exemple de programme donné, les adresses présentées à la RAM seront celles-ci :
- 0
- 1
- 100
- 2
- 3
- 101
- 4
- 5
- 102
- …
Les adresses de code sont globalement linéaires (0, 1, 2, 3, …), celles des données ne le sont pas (elles sont arbitraires). Il faut donc présenter sur le bus d’adresse RAM
- soit le compteur d’adresse pendant les deux premiers cycles (et on l’incrémente à chaque fois)
- soit le contenu du registre d’adresse (adresse de l’opérande à aller chercher) pendant le troisième cycle (et ici le compteur d’adresse ne doit pas être incrémenté)
donc : multiplexeur…
De plus, le compteur d’adresse doit être piloté par un signal INCR_PC : il n’est incrémenté que si INCR_PC est à l’état haut.
Le registre d’adresse est chargé au cycle numéro 2. Son contenu n’est utile qu’au cycle numéro 3. Il n’est donc pas nécessaire de le piloter avec un enable…Il peut rester tout le temps actif : son contenu sera indéterminé pendant les cycles 1 et 2, mais ce n’est pas grave, il n’est pas utilisé pendant ces cycles là…
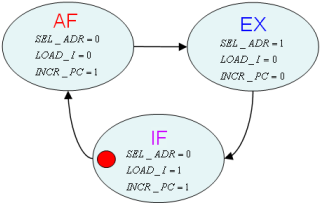
L’architecture globale est donc celle représentée sur la figure 1.8, et son graphe d’états en figure 1.9.
C’est, ici encore, une machine de Mealy, et ses équations sont :
LOAD_ACC = (I[7:0] <> STORE) ET (Etat = Ex)
WRITE = (I[7:0] == STORE) ET (Etat = Ex)
Réponse 6
1 Flags
La génération de C et Z est combinatoire et peut être effectuée par l’ALU.
Il suffit juste de rajouter deux registres 1 bits pour stocker ces deux signaux, pilotés par le même enable que l’accumulateur (LOAD_ACC, qu’on appellera maintenant LOAD_AZC). On considérera donc que Z et C font partie de l’accumulateur (qui devient donc un registre sur 10 bits : 8 de donnée, 1 pour Z, un pour C).
Remarque : le fonctionnement de Z et C ici n’est pas tout à fait standard !..
2 ADDC / SUBC
Il suffit de faire entrer C sur la retenue entrante de l’addition ou de la soustraction…
Réponse 7
Pour implémenter les sauts, il suffit de se donner la possibilité de remplacer le contenu de PC par la valeur lue en RAM.
PC devient donc un peu plus complexe. C’est globalement un compteur, mais :
- il est incrémenté si son signal de commande INCR_PC = 1
- il est chargé avec une nouvelle valeur si un signal de chargement LOAD_PC = 1
- Enfin, si LOAD_PC et INCR_PC valent 1, LOAD_PC a la priorité...
Ceci peut être implémenté comme indiqué en la figure 1.10.
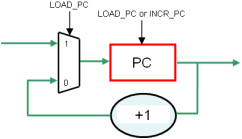
Pour simplifier les schémas, nous nommerons PC l'ensemble du bloc de la figure 1.10.
Il faut maintenant générer le signal LOAD_PC. Ce signal sera aussi généré par la machine à états CTRL. Le PC doit être remplacé lorsqu’on exécute un saut, et que le condition du saut est vérifiée. La nouvelle valeur est présente sur le bus de sortie de la RAM pendant le cycle 2.
On aura donc une équation du style :
(I[7:0] == JMP)
ou (I[7:0] == JNC et C == 0)
ou (I[7:0] == JNZ et Z == 0))
et (état = etat 2), alors 1,
sinon 0.
L’architecture globale est donc celle représentée sur la figure 1.11, avec un automate CTRL à peine modifié (même graphe d’état) représenté figure 1.12.
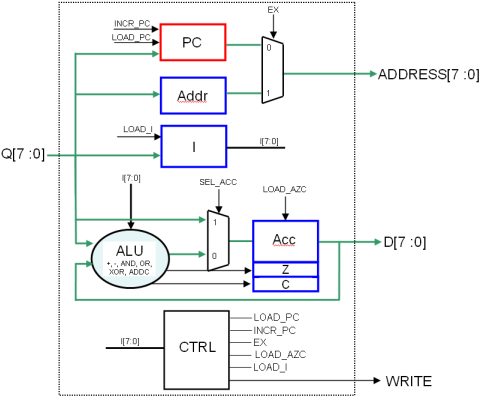
LOAD_ACC = (I[7:0] <> (STORE ou saut)) ET (Etat = Ex)
WRITE = (I[7:0] == STORE) ET (Etat = Ex)
LOAD_PC = si (I[7:0] == JMP ou I[7:0] == JNC et C == 0 ou I[7:0] == JNZ et Z == 0) et (état = Ad), alors 1, sinon 0
Réponse 8
L’instruction NOP ne fait rien. Elle n’a pas besoin d’opérande, et pourrait donc être stockée sur un seul octet (au lieu de deux pour les autres).
Mais cela compliquerait la gestion de l'automate pour générer les signaux LOAD_PC et INCR_PC. De plus, cela pourrait poser d’autres problèmes (cf. les optimisations).
On peut donc accepter de perdre un octet de mémoire, et ne rien changer à l’organisation de la mémoire. L’instruction NOP sera accompagnée d’un opérande qui ne servira a rien... Une instruction sera toujours exécutée en trois cycles. La seule modification de la machine à état sera l’équation suivante :
LOAD_ACC = (I[7:0] <> (STORE ou saut ou NOP)) ET (Etat = Ex)
Réponse 9
1 ROL / ROR
Ces opérations sont combinatoires et seront donc implémentées dans l’ALU.
Remarque : comme le NOP, elles ne nécessitent pas d’opérande. De même, pour garder une cohérence (nous optimiserons ça plus tard), on garde un codage des instructions sur deux octets. Pour ROR et ROL, le deuxième octet n’a pas de signification...
2 Sortie BZ
On ajoute un registre 1 bit, piloté par un signal d’enable appelé LOAD_BZ.
- l’entrée de ce registre est le bus de sortie de la RAM
- sa sortie est connectée à la broche de sortie buzzer du processeur...
LOAD_BZ sera généré par la machine à état, selon l’équation suivante : LOAD_BZ = (I[7:0] == OUT) et (état = EX)…
L’architecture globale est donc celle représentée sur la figure 1.13, avecun automate CTRL représenté figure 1.14.
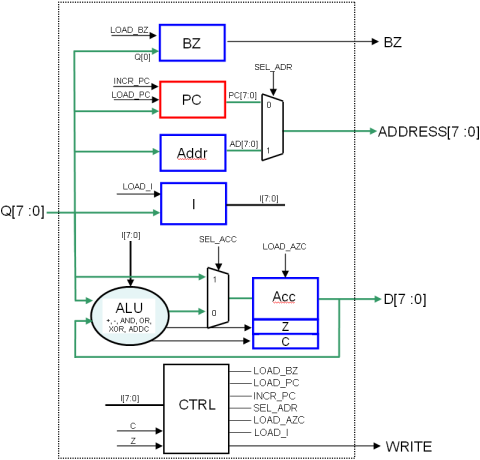
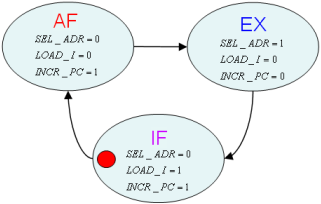
Les équation sont laissées en exercice au lecteur !..
Remarque : le signal SEL_ACC ne sort pas de CTRL sur le schéma : il peut être inclus, avec le multiplexeur qu’il pilote, dans l’ALU...
Réponses 10,11,12 et 13
Les réponses sont à trouver par le lecteur...